77.组合优化

算法公开课

《代码随想录》算法视频公开课 (opens new window)：组合问题的剪枝操作 (opens new window)，相信结合视频在看本篇题解，更有助于大家对本题的理解。

思路

在回溯算法：求组合问题！ (opens new window)中，我们通过回溯搜索法，解决了n个数中求k个数的组合问题。

文中的回溯法是可以剪枝优化的，本篇我们继续来看一下题目77. 组合。

链接：https://leetcode.cn/problems/combinations/

看本篇之前，需要先看回溯算法：求组合问题！ (opens new window)。

大家先回忆一下[77. 组合]给出的回溯法的代码：

class Solution {
private:
    vector<vector<int>> result; 
    vector<int> path; 
    void backtracking(int n, int k, int startIndex) {
        if (path.size() == k) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i <= n; i++) {
            path.push_back(i); 
            backtracking(n, k, i + 1); 
            path.pop_back(); 
        }
    }
public:
    vector<vector<int>> combine(int n, int k) {
        result.clear(); 
        path.clear();   
        backtracking(n, k, 1);
        return result;
    }
};

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

剪枝优化

我们说过，回溯法虽然是暴力搜索，但也有时候可以有点剪枝优化一下的。

在遍历的过程中有如下代码：

for (int i = startIndex; i <= n; i++) {
    path.push_back(i);
    backtracking(n, k, i + 1);
    path.pop_back();
}

1 2 3 4 5

这个遍历的范围是可以剪枝优化的，怎么优化呢？

来举一个例子，n = 4，k = 4的话，那么第一层for循环的时候，从元素2开始的遍历都没有意义了。在第二层for循环，从元素3开始的遍历都没有意义了。

这么说有点抽象，如图所示：

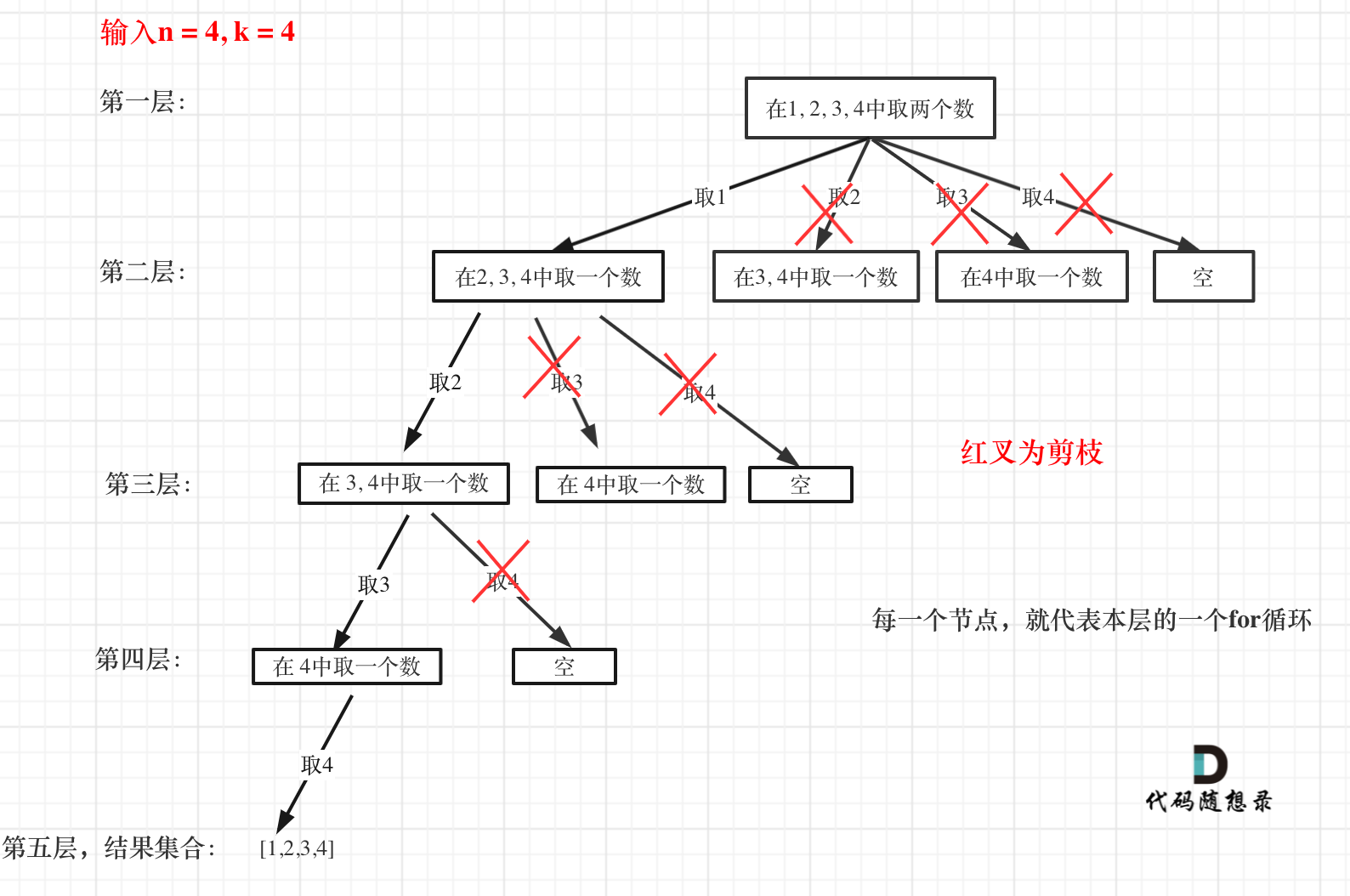
图中每一个节点（图中为矩形），就代表本层的一个for循环，那么每一层的for循环从第二个数开始遍历的话，都没有意义，都是无效遍历。

所以，可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。

如果for循环选择的起始位置之后的元素个数已经不足我们需要的元素个数了，那么就没有必要搜索了。

注意代码中i，就是for循环里选择的起始位置。

for (int i = startIndex; i <= n; i++) {

接下来看一下优化过程如下：

已经选择的元素个数：path.size();
所需需要的元素个数为: k - path.size();
列表中剩余元素（n-i） >= 所需需要的元素个数（k - path.size()）
在集合n中至多要从该起始位置 : i <= n - (k - path.size()) + 1，开始遍历

为什么有个+1呢，因为包括起始位置，我们要是一个左闭的集合。

举个例子，n = 4，k = 3，目前已经选取的元素为0（path.size为0），n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。

从2开始搜索都是合理的，可以是组合[2, 3, 4]。

这里大家想不懂的话，建议也举一个例子，就知道是不是要+1了。

所以优化之后的for循环是：

for (int i = startIndex; i <= n - (k - path.size()) + 1; i++)

优化后整体代码如下：

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(int n, int k, int startIndex) {
        if (path.size() == k) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) { 
            path.push_back(i); 
            backtracking(n, k, i + 1);
            path.pop_back(); 
        }
    }
public:
    vector<vector<int>> combine(int n, int k) {
        backtracking(n, k, 1);
        return result;
    }
};

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

时间复杂度: O(n * 2^n)
空间复杂度: O(n)

总结

本篇我们针对求组合问题的回溯法代码做了剪枝优化，这个优化如果不画图的话，其实不好理解，也不好讲清楚。

所以我依然是把整个回溯过程抽象为一棵树形结构，然后可以直观的看出，剪枝究竟是剪的哪里。

就酱，学到了就帮Carl转发一下吧，让更多的同学知道这里！

其他语言版本

Java

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> combine(int n, int k) {
        combineHelper(n, k, 1);
        return result;
    }
    
    private void combineHelper(int n, int k, int startIndex){
        
        if (path.size() == k){
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = startIndex; i <= n - (k - path.size()) + 1; i++){
            path.add(i);
            combineHelper(n, k, i + 1);
            path.removeLast();
        }
    }
}

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

Python

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        result = []  
        self.backtracking(n, k, 1, [], result)
        return result
    def backtracking(self, n, k, startIndex, path, result):
        if len(path) == k:
            result.append(path[:])
            return
        for i in range(startIndex, n - (k - len(path)) + 2):  
            path.append(i)  
            self.backtracking(n, k, i + 1, path, result)
            path.pop()

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

Go

var (
    path []int
    res  [][]int
)
func combine(n int, k int) [][]int {
    path, res = make([]int, 0, k), make([][]int, 0)
    dfs(n, k, 1)
    return res
}
func dfs(n int, k int, start int) {
    if len(path) == k {  
        tmp := make([]int, k)
        copy(tmp, path)
        res = append(res, tmp)
        return 
    }
    for i := start; i <= n - (k-len(path)) + 1; i++ {  
        path = append(path, i)
        dfs(n, k, i+1)
        path = path[:len(path)-1]
    }
}

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

JavaScript

var combine = function(n, k) {
    const res = [], path = [];
    backtracking(n, k, 1);
    return res;
    function backtracking (n, k, i){
        const len = path.length;
        if(len === k) {
            res.push(Array.from(path));
            return;
        }
        for(let a = i; a <= n + len - k + 1; a++) {
            path.push(a);
            backtracking(n, k, a + 1);
            path.pop();
        }
    }
};

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

TypeScript

function combine(n: number, k: number): number[][] {
    let resArr: number[][] = [];
    function backTracking(n: number, k: number, startIndex: number, tempArr: number[]): void {
        if (tempArr.length === k) {
            resArr.push(tempArr.slice());
            return;
        }
        for (let i = startIndex; i <= n - k + 1 + tempArr.length; i++) {
            tempArr.push(i);
            backTracking(n, k, i + 1, tempArr);
            tempArr.pop();
        }
    }
    backTracking(n, k, 1, []);
    return resArr;
};

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

Rust

impl Solution {
    fn backtracking(result: &mut Vec<Vec<i32>>, path: &mut Vec<i32>, n: i32, k: i32, start_index: i32) {
        let len= path.len() as i32;
        if len == k{
            result.push(path.to_vec());
            return;
        }
	
        for i in start_index..= n - (k - len) + 1 {
            path.push(i);
            Self::backtracking(result, path, n, k, i+1);
            path.pop();
        }
    }
    pub fn combine(n: i32, k: i32) -> Vec<Vec<i32>> {
        let mut result = vec![];
        let mut path = vec![];
        Self::backtracking(&mut result, &mut path, n, k, 1);
        result
    }
}

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

C

int* path;
int pathTop;
int** ans;
int ansTop;
void backtracking(int n, int k,int startIndex) {
    
    if(pathTop == k) {
        
        
        int* temp = (int*)malloc(sizeof(int) * k);
        int i;
        for(i = 0; i < k; i++) {
            temp[i] = path[i];
        }
        ans[ansTop++] = temp;
        return ;
    }
    int j;
    for(j = startIndex; j <= n- (k - pathTop) + 1;j++) {
        
        path[pathTop++] = j;
        
        backtracking(n, k, j + 1);
        
        pathTop--;
    }
}
int** combine(int n, int k, int* returnSize, int** returnColumnSizes){
    
    path = (int*)malloc(sizeof(int) * k);
    
    ans = (int**)malloc(sizeof(int*) * 10000);
    pathTop = ansTop = 0;
    
    backtracking(n, k, 1);
    
    *returnSize = ansTop;
    
    *returnColumnSizes = (int*)malloc(sizeof(int) *(*returnSize));
    int i;
    for(i = 0; i < *returnSize; i++) {
        (*returnColumnSizes)[i] = k;
    }
    
    return ans;
}

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50

Swift

func combine(_ n: Int, _ k: Int) -> [[Int]] {
    var path = [Int]()
    var result = [[Int]]()
    func backtracking(start: Int) {
        
        if path.count == k {
            result.append(path)
            return
        }
        
        
        
        let end = n - (k - path.count) + 1
        guard start <= end else { return }
        for i in start ... end {
            path.append(i) 
            backtracking(start: i + 1) 
            path.removeLast() 
        }
    }
    backtracking(start: 1)
    return result
}